La Torre di Hanoi (anche conosciuta come Torre di Lucas dal nome del suo inventore) è un rompicapo matematico composto da tre paletti e un certo numero di dischi di grandezza decrescente, che possono essere infilati in uno qualsiasi dei paletti.
Il gioco inizia con tutti i dischi incolonnati su un paletto in ordine decrescente, in modo da formare un cono. Lo scopo del gioco è portare tutti i dischi su un paletto diverso, potendo spostare solo un disco alla volta e potendo mettere un disco solo su un altro disco più grande, mai su uno più piccolo.
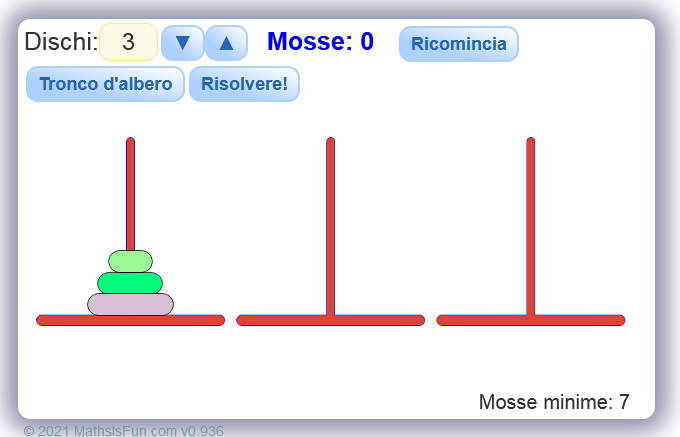
La Torre di Hanoi.
Il gioco fu inventato nel 1883[1] dal matematico francese Édouard Lucas che diffuse il gioco sotto lo pseudonimo di N. Claus de Siam, mandarino del collegio di Li-Sou-Stian.
La leggenda secondo la quale in un tempio Indù alcuni monaci sono costantemente impegnati a spostare su tre colonne di diamante 64 dischi d’oro secondo le regole della Torre di Hanoi (a volte chiamata Torre di Brahmā), è stata inventata dalla ditta che per prima ha messo in commercio il rompicapo.
La leggenda narra che quando i monaci completeranno il lavoro, il mondo finirà. Esistono anche versioni videoludiche del rompicapo.
Scopo del gioco.
Lo scopo del gioco è spostare tutti i dischi sulla Torre 3 (con il mouse).
Ma non puoi posizionare un disco più grande su un disco più piccolo.
La proprietà matematica base è che il numero minimo di mosse necessarie per completare il gioco è 2 n − 1 {\displaystyle 2^{n}-1} 2^{n}-1, dove n è il numero di dischi. Ad esempio avendo 3 dischi, il numero di mosse minime è 7. Di conseguenza, secondo la leggenda, i monaci di Hanoi dovrebbero effettuare almeno 18.446.744.073.709.551.615 mosse prima che il mondo finisca, essendo n = 64 {\displaystyle n=64} n=64. In altre parole, anche supponendo che i monaci facciano una mossa al secondo il mondo finirà tra 5.845.580.504 secoli.[7]
La soluzione.

La soluzione generale è data dall’algoritmo seguente.
Algoritmo ricorsivo
La soluzione base del gioco della torre di Hanoi si formula in modo ricorsivo.
Siano i paletti etichettati con A, B e C, e i dischi numerati da 1 (il più piccolo) a n (il più grande). L’algoritmo si esprime come segue:
Sposta i primi n-1 dischi da A a B. (Questo lascia il disco n da solo sul paletto A)
Sposta il disco n-1 da A a C
Sposta n-1 dischi da B a C
Per spostare n dischi si richiede di compiere un’operazione elementare (spostamento di un singolo disco) ed una complessa, ossia lo spostamento di n-1 dischi. Tuttavia anche questa operazione si risolve nello stesso modo, richiedendo come operazione complessa lo spostamento di n-2 dischi. Iterando questo ragionamento si riduce il processo complesso ad uno elementare, ovvero lo spostamento di n-(n-1)=1 disco.
Questo è un algoritmo ricorsivo, di complessità esponenziale.
È interessante notare che il rompicapo è risolvibile per qualsiasi “n”, con una dimostrazione per ricorrenza: Supponiamo di avere una torre in A composta da N dischi, e supponiamo che N sia il numero massimo di dischi ammessi per risolvere il gioco. Al termine dello spostamento della torre da A a B, aggiungiamo un ulteriore disco ad A, di grandezza pari a N+1, e ipotizziamo che questo disco sia stato fermo tutto il tempo sotto gli altri. A questo punto, spostiamo semplicemente il disco da A a C, e certamente riusciremo a spostare la torre da B a C, seguendo gli stessi passaggi che si sono resi necessari per spostarla da A a B. Avendo dimostrato che una torre di N dischi è spostabile da una colonna all’altra, è dimostrato che si può spostare anche una torre di N+1 dischi.
Problema Generalizzato.
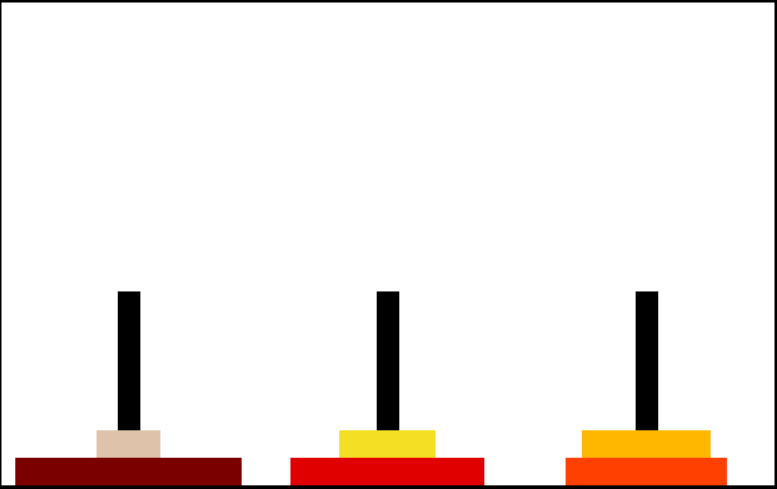
Il problema può essere generalizzato, supponendo ad esempio che il numero dei paletti non sia fissato a tre ma genericamente estendibile.
Supposta tale generalizzazione sono noti esempi di strategie ottimali per il completamento del gioco, sotto specifiche ipotesi, fin dal 1941. Esse sono state trovati separatamente da diversi autori.
La dimostrazione che tali strategie sono quelle ottimali in ogni condizione è invece un risultato del 2017. La principale difficoltà della dimostrazione era implicata dalla non unicità, nel caso con più di tre paletti, della strategia ottimale da seguire durante la risoluzione. Nel caso generale, di fatti, dopo ogni mossa è possibile cambiare strategia pur restando nel numero minimo di quelle necessarie a risolvere il puzzle, creando un complesso albero di percorsi risolutivi che impiegano lo stesso numero minimo di passi per risolvere il problema. Tale non unicità non è da intendersi nel ovvio senso delle permutazioni, ma nel modo più generale possibile